THAT
This is THAT.

THAT (The Analog Thing) is an analogue computer. Other than digital computers, analogue computers do not quantify everything into discrete 0 and 1 values, but use continuous value ranges expressed in voltages. They don’t compute algorithms, but simulate models expressed in differential equations. That means math, a lot of it.
Analogue computers have been around for a long time. While Leibniz was first to propose the binary system in the 17th century, the oldest analogue computer known today is the Antikythera mechanism. This was built more than 2000 years ago for astronomical predictions. The thing with analogue computers is, they don’t need electricity. Cogs and wheels will do, as in the Antikythera mechanism. Or water. (If you have a mechanical wristwatch or classic “grandfather’s clock”, voilà, you have yourself a specialised analogue computer.)
Electronic analogue computers like THAT are meant to be a versatile tool for, as mentioned, modelling and simulating systems expressed as differential equations. They consist of surprisingly simple circuits that sum, multiply, invert, and integrate voltages over time. Programming is done by plugging wires into sockets. Outputs are typically visualised using an oscilloscope.
Here’s a photo of the basic setup - no “code” has been entered. The second photo shows the, well, syntactic elements of the programming language, so to speak.


Let’s look at an example: radioactive decay. (It’s explained on p. 10 in the THAT intro manual.) This is a simple differential equation with two coefficients: initial amount, and decay rate. Here’s the configured THAT. If you look close, you can see that it indeed uses two coefficients (top left), one integrator (top, a bit to the right), and one inverter (right).

And guess what - it works! Some fiddling with the oscilloscope settings later, I was able to see my first analogue computer program run. Messing around with the coefficients a bit, I could also change the result in real time.


Something was odd about the signal though. Taking a close look at the photo below, you’ll notice that the main yellow line is surrounded by a fuzzy yellow shadow.
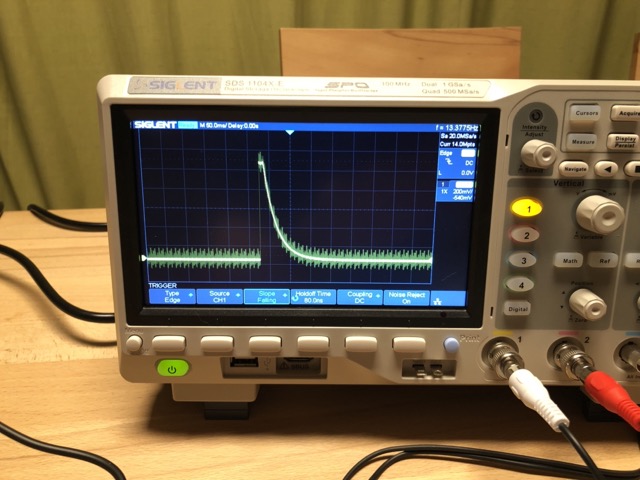
OK - this is where things get really interesting. Remember we’re in the realm of voltages measured continuously over time, not in the neatly 0-1-compartmentalised world of digital computing. A brief exchange with a friend who’s more of an electrical engineer than I am taught me that signal quality matters, and so does power supply quality.
In my first experiment, I was powering THAT using a standard garden variety USB charger, and apparently it’s not well grounded, leading to a distorted and somewhat modulated voltage. That has an impact on the output signal.
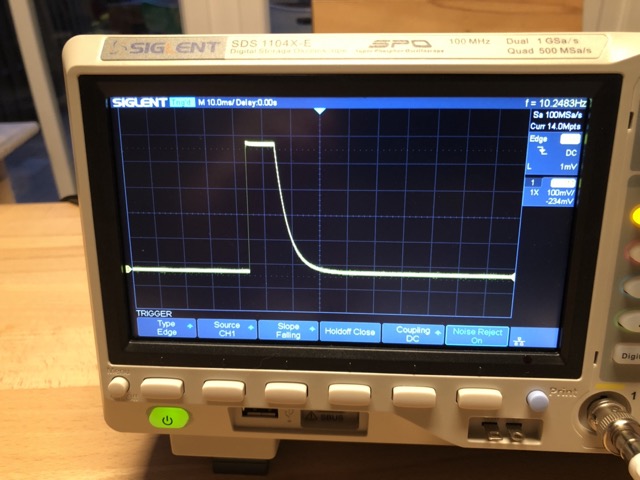
My friend suggested to use a power bank (no AC involved), but I didn’t have a charged one. The highest quality AC/DC power supply I had available was an Apple MacBook one, so I used that. Behold. Now that’s what I call a clean signal.
My next venture took me to the Euler Spiral, which is supposedly a beautiful 2D curve, and even a lot of fiddling didn’t get me anywhere closer to the expected result than this ...
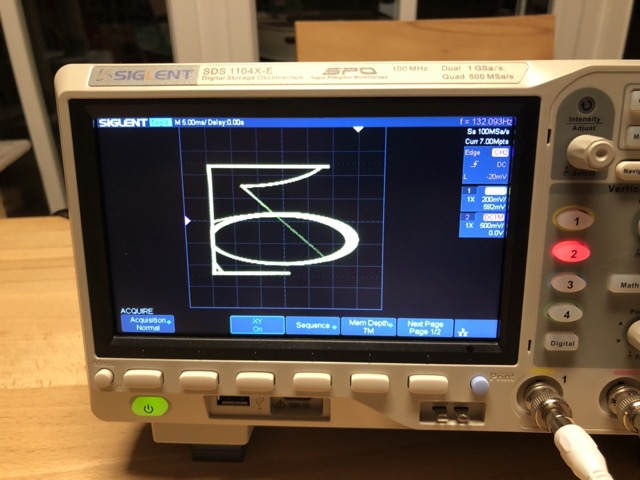
... which is a bit disappointing. It looks like the signal is cut off somehow. I chatted some more with my friend, and delved into the documentation a bit, and observed that THAT is constantly in overload mode while running this simulation. We found the RCA ports on THAT cap voltages for consumption by audio devices as one possible segue to USB oscilloscopes. I will next try to connect the outputs directly to the oscilloscope. Stay tuned.
Tags: the-nerdy-bit